HI – MY NAME IS ALPHA LIMA ALPHA NOVEMBER!
Math in Aviation – Class 11 – Middle Lesson
That’s Alan actually! Have you ever wondered about that mystical radio code on cop shows where they quote a car number plate as ‘foxtrot, Oscar, whisky”, and such like? Learning this is one of the bonuses of teaching a Maths in Aviation 3-week middle lesson. This, and lots more esoteric content helps keep the Spirit alive in this final maths unit for Class 11.
The Phonetic Alphabet is used for clarity, many English letters sounding so similar as they do, like B, C, D, E and so on. This ‘ee’ sound is evidence of the Mercury, or egoistic element in our alphabet, the letters ultimately deriving from the human being – the Ego – as they do.
Rudolf Steiner nominates E as the vowel of this, appropriate for an aviation lesson, winged god. But I stray from Maths to English; though his integration of concepts often livens up a lesson; exploit it while you can. After all, calculation of various kinds enter other disciplines!
A ALPHA, B BROAVO, C CHARLIE, D DELTA, E ECHO, F FROXTROT, G GOLF, H HOTEL, I INDIA, J JULIET, K KILO, M MIKE, N NOVEMBER O OSCAR, P PAPA, Q QUEBEC, R ROMEO, S SIERRA, T TANGO U UNIFORM, V VICTOR, W WHISKY, X X-RAY, Y YANKEE, Z ZULU. And that’s the alpha and zulu of it!
The aviation industry also relies up Morse Code as a back-up communications system. The students should be at least familiar with this, even if they don’t laboriously learn it: A .- B -… C-.- D -.. E . F ..-. G –. H …. I .. J .— K -.- L .-.. M – N – O — P .–. Q –.- R .- S … T – U ..- V …- W .—X -..- Y -.—Z –.. !! The important one to learn, for everyone, is the universal code for a dire emergency – Sierra Oscar Sierra, SOS, in mores, … — … ! “MAYDAY!” is also used.
While on lists, there are the Multipliers: we begin in the center with – aptly – Centi, which means times one hundredth, then there’s Kilo X 1000, Mega X 1,000,000 and GiGa X 1,000,000,000 (1 billion).
Moving from centi downwards, we have Milli X one thousandth (1 over 1000), Micro X one millionth, Nana X one billionth, and finally Pico X one thousand billionth (trillionth). This last doesn’t necessarily mean small (though it usually does), one Pico of, say, the number of stars in one constellation of the zodiac, or grains of sand in the Simpson’s Desert, is still an infinitely large number.
So, now we’re ready for take-off. In aviation there are two basic principles of flight – or “lift”: 1. Aerostatic or Displacement Lift is based on Archimedes theory that “A body immersed in a gas or liquid is buoyed by a force equal to the weight of liquid or gas displaced.” Eureka!
- Aerodynamics or Wing Lift is obtained from the flow of air moving over a wing. There is a 13th Century design left to us of a flight machine, four air-filled copper globes attached to a gondola – romantic if somewhat impractical! Leonardo da Vinci sketched many, more plausible, designs for aircraft after studying bird flight. These were far too advanced to be comprehended by this 16th Century contemporaries.
But back to Displacement Lift; once airborne, a balloon is swept along with the wind at the same speed and direction. It must have an engine before its flight direction can be controlled by a rudder. In 1852 Frenchman Henri Gifford prepared the first powered balloon flight with a 48m long by 12m diameter balloon with a 3hp motor attached. This proved to be at least semi-controllable. Brazilian Alberto Santos-Dumont flew around the Eiffel Tower in 1901 in a petrol engine airship.
Count Ferdinand von Zeppelin built his first eponymous airship in 1899. Subsequent Zeppelins became the most successful fully controlled airships in the world. There are three kinds of “balloons”:
- Non-rigid, the shape held together solely by air pressure.
- Semi-rigid, with a ridged keel only.
- Rigid – a fully framed airship, like the benighted The development of these giants was aided by the invention by the Germans of Duralum, an alloy one third the weight of steel. This provided for an extremely light-weight frame.
The evolution of Aerodynamic Lift is well documented, and the students should be acquainted with this; from Orville and Wilbur Wright, through to the difficulties of World War I commanders appreciating the potential of aircraft in war. In spite of their intransigence, development and production of aircraft escalated, and by 1918 Britain, to cite just one combatant, was churning out 30,000 planes a day.
Through necessity, speed, power, height and stability all increased. Four years of war had seen moss flight move from a dream to a reality; pilots became honored, rather than being thought of as mere crazy exhibitionists. KLM Royal Dutch Airlines, founded in 1919, was the first commercial people and products aerial transporter, and is still one of the biggest and best. Then there was Lufthansa, BOAC and our own “Spirit of Australia”, Qantas – Queensland And Northern Territory Aerial Service; the safest airline in the world, with not a single flight fatality since its founding in 1920!
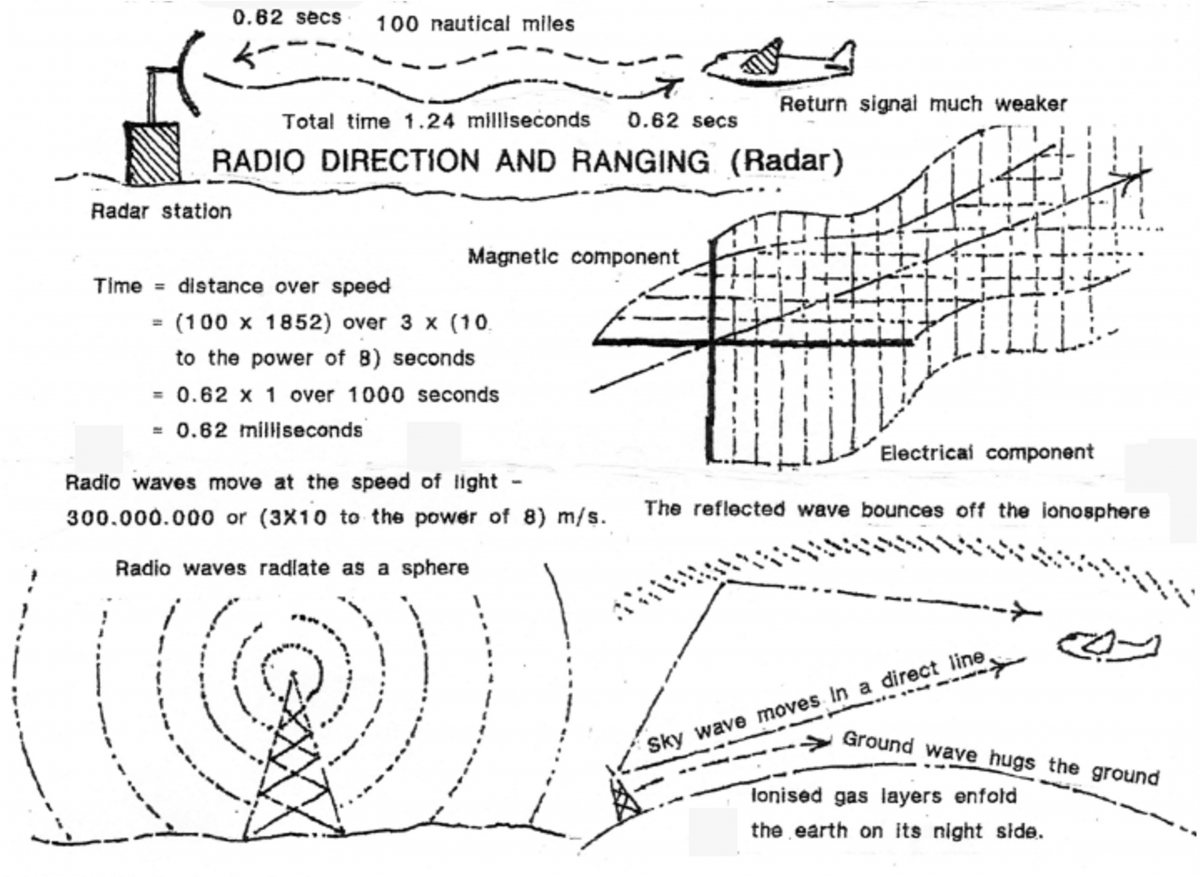
In 1939, Hitler unleashed the Luftwaffe (‘air weapon’) on a stunned Europe. Ultimately much of the war was won or lost on the superiority of air power. The development of pressurized cabins, air-cooled engines, radio and radar systems led to both military and civil aircraft being increasingly advanced and multi-purpose.
In many cases knowledge of physiology had to keep pace with that of technology as man left the familiarity of solid earth in defying gravity. The senses often play tricks when flying; these can take the form of seeing things that aren’t there; or of loss of orientation in space. When flying through cloud at zero visibility, it is impossible to tell, without consulting the aircraft’s instruments, whether one is even flying upside-down or not.
Generally the eyes are the most crucial sense in flying – as they are with birds, the best sighted of all creatures. Further back still in the evolution of the eyes, the first sighted creatures were also the first winged, the ubiquitous Arthropods, like moths. This sight factor is the origin of all those military myths about night-flying pilots eating lots of carrots to hone their nocturnal vision. Even so, one must be aware of some of the tricks the yes can play when aloft; one is the “blind spot”, where the optic nerve passes out of the eye to the brain.
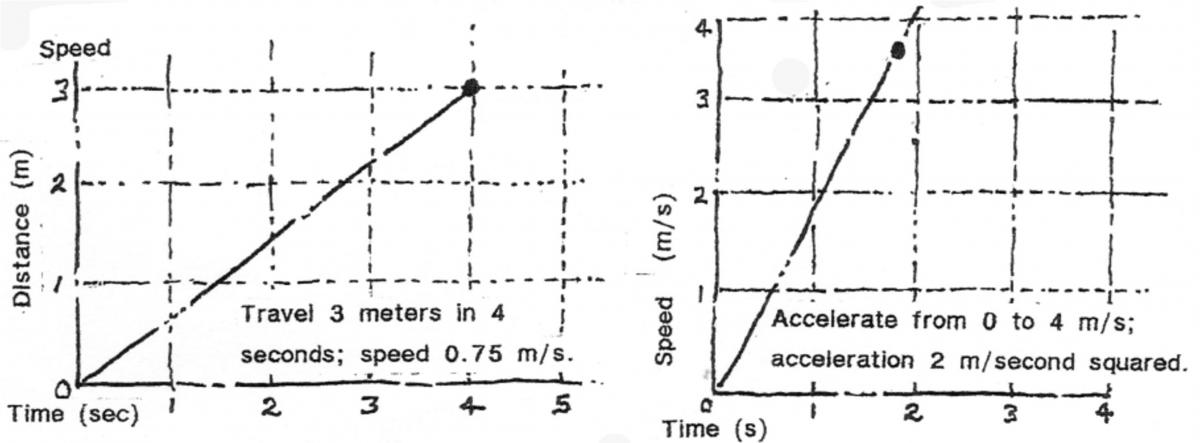
Then there are the ears, not for hearing, but vital for our perception of equilibrium. When we accelerate in any direction, the fluid in the labyrinth of the middle ear semi-circular canals moves. This causes tiny hairs to bend; which alerts the brain to the movement. These hairs are capped with an even tinier highly sensitive crystal, the Capula. Acceleration is calculated as the G Force, with increasing degrees leading to different physical responses. At -2 Gs, a Red-out is experienced, caused by being forced to look through the bottom eyelid. 4.5 Gs lead to a Grey-out, which is lack of oxygen in the eyes, making everything appear grey. 5 Gs lead to the self-explanatory Blackout, due to oxygen deprivation in the brain. A Whiteout is similar to that experienced with snow blindness. In the air is usually caused by white cloud (or surface snow). The graph following demonstrates routine speed and acceleration calculations pilots and aeronautical navigators must continually make:
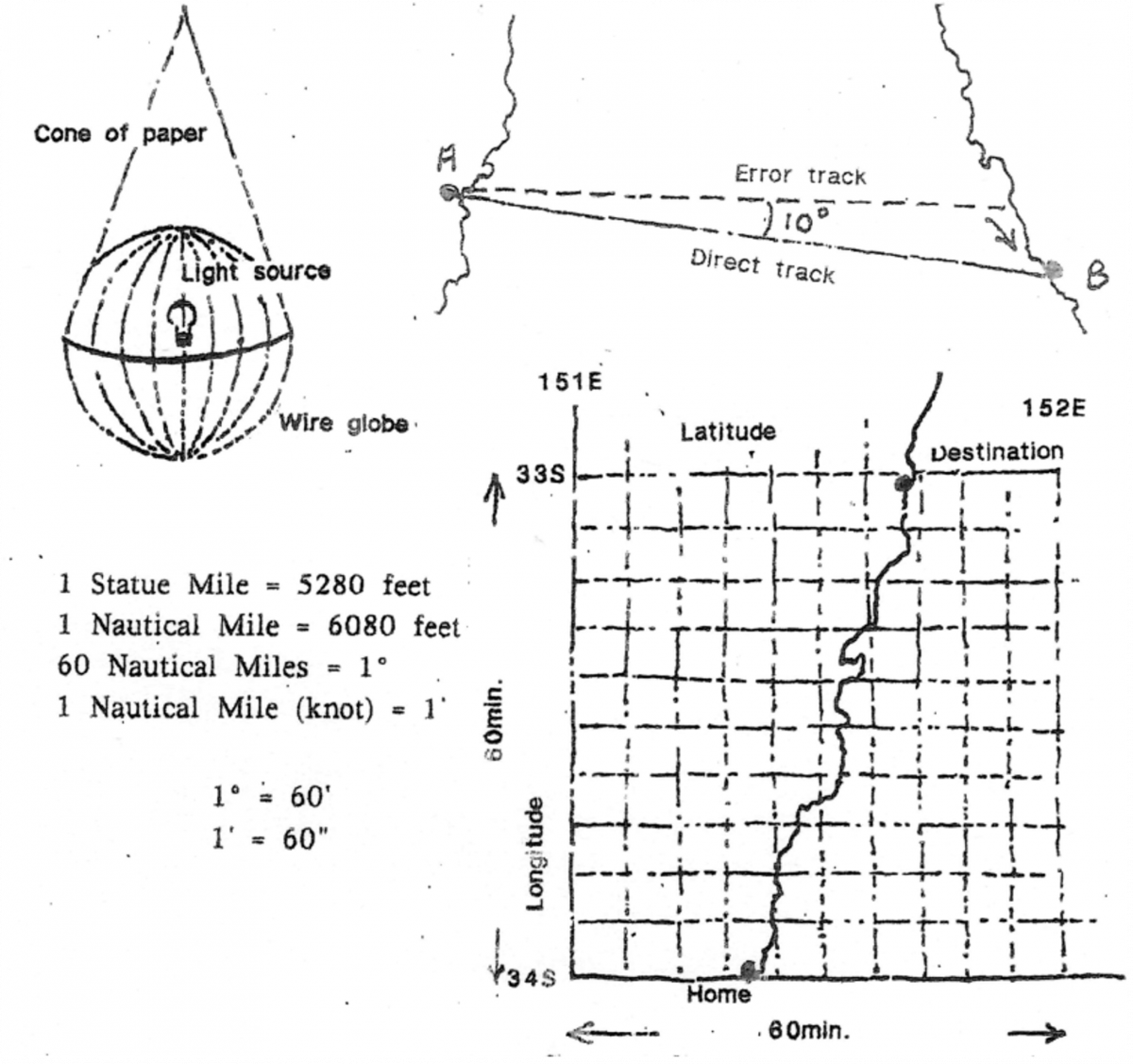
Sir Francis Chichester circumnavigated the globe in a Tiger Moth, a tiny vintage biplane. This aircraft did not have any modern navigation equipment; so to overcome the problem, especially while flying over water, he used “navigation by deliberate error”. He would purposely steer 10° of so to starboard or port of the direct track, so that he knew which way to turn when he arrived at the coast, mountain range, whatever. This way there is a marginal increase in distance, but at least one does ultimately arrive at one’s destination! The basic map used by pilots for visual navigation is the Lambert’s Conformal (conical) Projections.
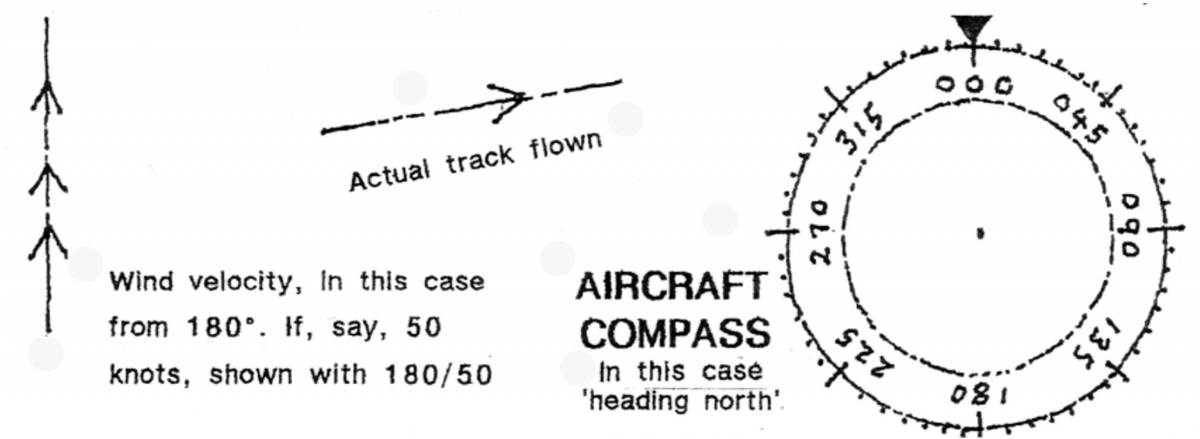
The Indicated Air Speed (IAS) is the speed of the aircraft relative to the airflow around it. True Air Speed (TAS) is the indicated airspeed compensated for the change in atmosphere and altitude. Groundspeed (GS), is the speed of the aircraft relative to the ground. This is the TAS, but making allowance for altitude. For example, at 10,000 feet altitude, IAS = 240 knots, therefore TAS = 280 knots. 1.The Aircraft heading is the magnetic bearing to which the aircraft is pointing. 2. The Aircraft Planned Track is the direction intended to travel. 3. The Track made Good is the actual track flown 4 Wind Velocity.
Communication is an important function in modern aviation. Radios are the most common facility to keep air-to-air or air-to-ground contact. A common dialogue might be: “You are cleared to land.” – “Please advise on the surface wind and your location.” Radio waves are created by electrical energy, combined with a type of magnetic energy. These speed through the air from a transmitter to a receiver; together they are known as electromagnetic waves, and are represented thus:
Horsepower and Thrust is the power that engines supply to push an aircraft forward and upward. Most engines, and all engines in aircraft, come under the general heading of ‘heat engines’: such as steam, piston and jet engines, to accord with the evolution of non-animal horsepower. Heat engines obtain their power from a high-pressure hot gas which is ultimately released into the atmosphere. Most aircraft engines are one of four kinds: piston, jet turbine, turboprop and fan jet.
Modern high-performance Gliders are one of the most efficient aircraft of all, as they employ the most advanced aero-dynamics and structures. It is also one of the simplest and safest forms of flying, using rising currents of hot air – thermals. The most common of these hot air columns are: 1. Sea breeze thermals. 2. Cumulus thermals (at the front of cumulus rain clouds); these are wet thermals. 3. Dry thermals occur when hot air rises over barren stretches of land, like ploughed fields or large carparks. 4. Lee waves; such as when hot air currents rise off mountains at thousands of feet per minute.
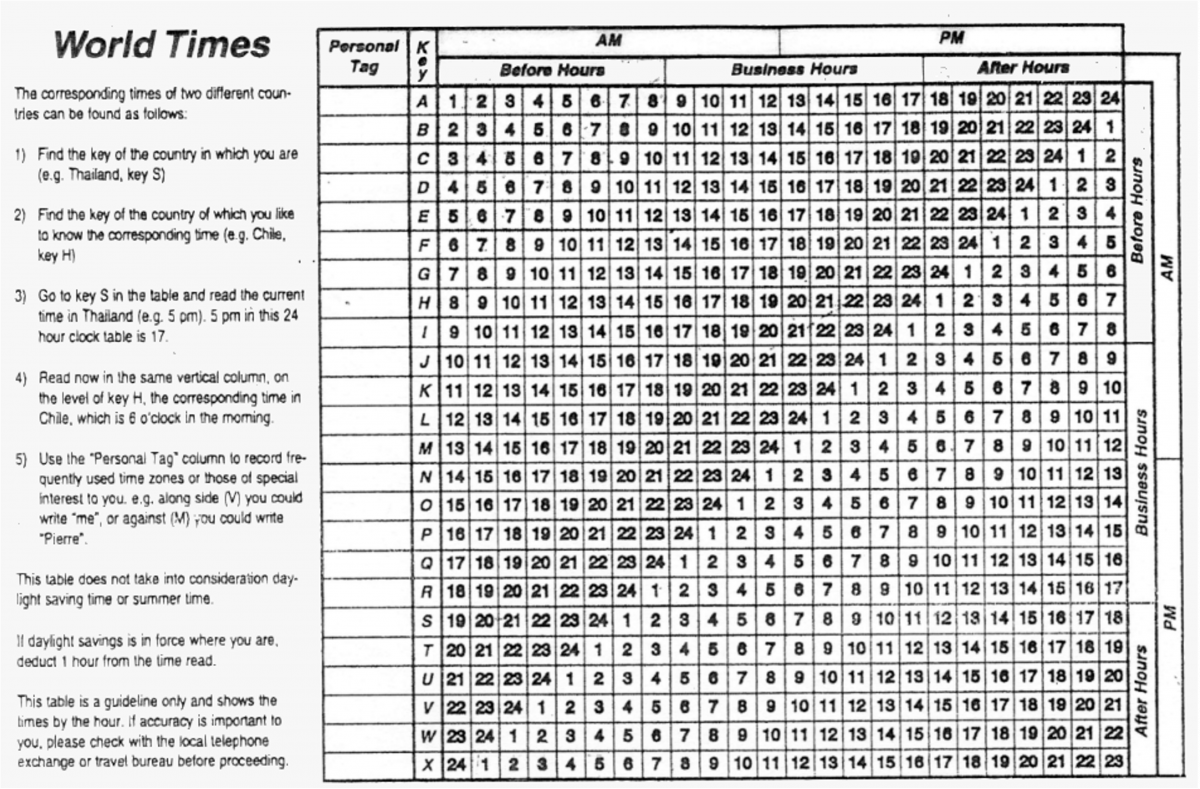
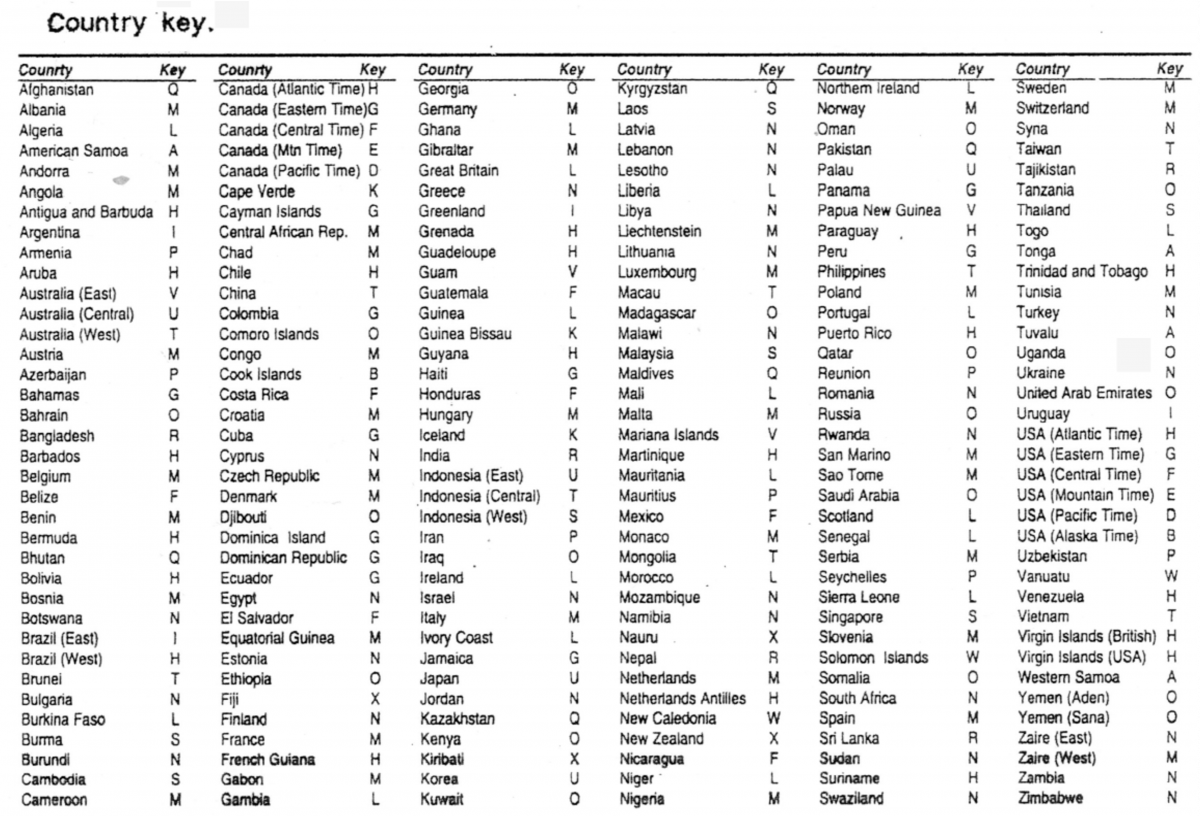
Zulu or London Time is the uniform universal aviation standard, denoting a world mean or Greenwich time; also known as UTC – International Time Convention. All longitudinal navigation, since the Age of Discovery, has had to have a chronometer set on Zulu time as a reference point to their own position, hence time. Students should perform calculations working out Zulu time at different times and places. Of course the 24-hour clock is almost exclusively employed in the aviation industry.
All aviators must be familiar with the official System of Measurement (SI): Time – second – s: Weight – kilogram – kg; Length – meters – m; Volume – cubic meters – m3; Force – mass x acceleration – Newtons – N; Velocity – meters per second – v; Temperature – degrees – °C; Voltage – volts – v; Current – Amps – A; Resistance – Ohms – ; Pressure – force per unit area – N over m squared.
No treatise on aviation, maths or otherwise, taught to Australian students would be complete without mention of our greatest flyer, Sire Charles Kingsford-Smith. He was the most distinguished pilot of his time, the barnstorming ‘30s. He was born in Brisbane in 1897 and learned to fly in World War I – at the tender age of 17.
‘Smithy’s’ reputation was based on varying attempts at being the first to pilot one of the flimsy airplanes of the time from seemingly impossible points A to B. With Charles Ulm, he created Australian National Airways, which became the most successful, reliable airline of the 1920s.
In the now legendary and aptly names Southern Cross, Smithy, Ulm and two crew became the first to conquer the most formidable natural barrier of all, the mighty Pacific Ocean, from San Francisco to Brisbane. Their ability to ‘fly blind’ using celestial and other navigation was uncanny. For this achievement, this magnificent man in his flying machine was knighted Smithy also achieved the first crossing of the Tasman Sea. As well he flew around the whole continent of Australia in just 12 days – an unprecedented circumnavigation. Cheering crowds greeted him when he landed at Mascot Airport – later deservedly named Kingsford-Smith Airport.
In their failed attempt to be the first to circumnavigate the world by air, Smithy and Ulm crashed-landed in Western Australia. They were found safe two weeks later; but received criticism for indirectly causing the death of two searchers. When the indominable Smithy attempted an England-to-Sydney record in 1934, he disappeared somewhere off the coast of Burma; to the profound grief of not only proud Australians, but lovers of flying and Boy’s Own adventure the world over.
The aforementioned Qantas was at first an outback service in Northern Australia, but soon spread to all capitals. Qantas (the only English word beginning with a Q not followed by a U) had the first flying boat service, based at Rose Bay; but their greatest achievement was, in 1957, their Australia-America-England around the world service.
By 1960, Qantas had the largest fleet of Boeing 707s in the world. When Hudson Fyshe, one of the airline’s founders, took delivery of the spectacular new – and still the best, a whole quarter century later – Jumbo Jets in the 1970s, Qantas was truly up there with the best international world airlines. What a far cry this was, in less than one hundred years, from James Glaisher and Henry Coxwell, who in 1862 were sucked up 30,000 feet (a Jumbo’s cruising altitude!) through the center of a cumulonimbus thunderhead!
The higher altitude mathematics ascends in senior high school, the harder it becomes to categorize it. So many areas of study employ maths as a tool; so many areas of maths are exclusively devoted to the evolution and service of specific disciplines. So maths programming can become a rather rubbery exercise; all my curriculum recommendations being only that – recommendations.
Is this unit Aviation? Or Maths in Aviation? Which areas of the vast tableau of aviation? Is it perhaps a strand of Engineering? Or Geometry? Whatever, I have chosen Maths in Aviation – with an emphasis on the maths over the aviation – to be scheduled in the Middle Lessons, with their strong vocational element.
Middle lessons also appeal to the central rhythmic system, or heart forces of the students. The aviation industry is one which energizes this feeling life to the point of obsession with many. Pilots often attest to loving flying, and the sleek aircraft they fly, more than all else in their apparently limited lives. Of the four Middle Lesson strands of Professions-Ego, cultural-Astral, Service-Etheric and Industrial-Physical, Maths in aviation seems to make a safe 3-point landing in the last, the Industrial. Most of the calculations in aviation apply to ‘physical’ phenomena, be int weather, fuselage design or flight plans.
Of the three Industrial strands of Primary, Secondary and Tertiary Industries, again the choice is far from self-evident. Maths in Aviation is certainly not the first – but it could be a Tertiary Industry, as in the transport and defense. But in the creation of the aircraft and the infrastructure of flying, which we are mostly concerned with, Maths in Aviation seems to be best housed in the Secondary Industry hanger.
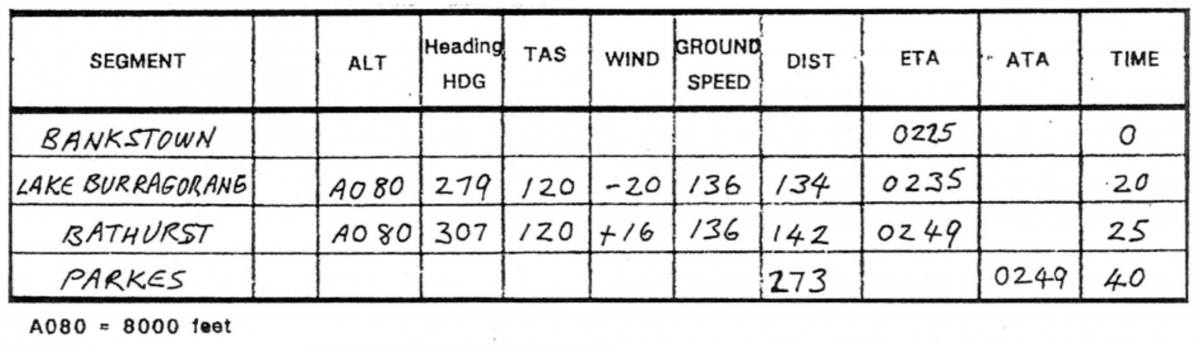
A salutary exercise for my class was the plotting of a course; this was to show the many contingencies that have to be taken into account. To get from point A to B in an airplane, one doesn’t just point the nose in the – imagined – desired direction, have a look out the window now and then, and arrive on time and on location. One must first have a flight plan, then an in-flight log. The following is a flight log worked out by the students for a flight from Bankstown Aerodrome in Sydney to Parks in Central Western NSW:
Students in the author’s class swagger around in their flying suits, boots and helmets: from an excursion to Richmond RAAF base…
As well as the maths involved in navigation in aviation, the Geometry of Flight can be explored. My class began with learning the conventions of technical drawing in relation to aircraft engineering with a 3-view orthographic projection of a Lear Jet: The exercise contained scaling up or down; dimensioning; titles; aircraft terminology in both form and function, like tail plane, fuselage, rudder, elevator, axii, aileron, pitch, yaw, roll.
Emphasis was placed on drawing technique, such as the conventions of line firming, borders, information baseplate and lettering. To balance the Aviation experience as not only a conceptual, but a practical one, the class went Hang Gliding as one of their Friday sports for the term.
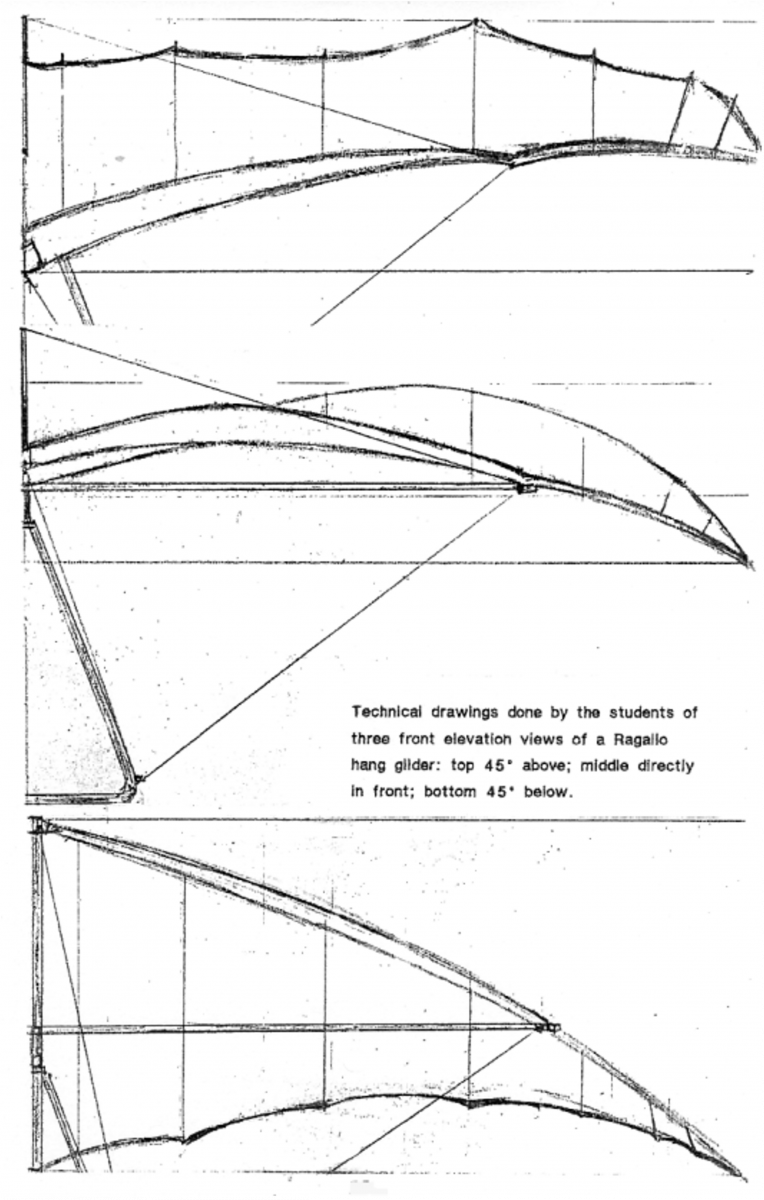
One result of this hands-on-the-bar, feet-off-the-ground knowledge was a more sophisticated embellishment of their drawings, especially relating to the shape, form and structure (astral, etheric, physical) of flight. One of the drawings of course being of a hang glider. In this there were four views, all in front elevation, designed to capture the inherent movement of a Ragallo hang glider, both in descent and ascent.
The first view was from 45° above; the second directly in front, the third 45° below, the fourth underneath. Aspects of projection and shading were demonstrated, as was the evolution of the aerodynamic curves.
To exploit the “integration of knowledge” principles, there were many references to bird physiology, such as the behavior of air molecules providing low pressure, hence lift, as they flow over the curved surface of a wing. As an exercise in independent research, the students each chose a particular plane to draw, in a three-quarter view. Considerable measuring, scaling and other technical drawing skills were required for this.
Also a series of smaller drawings was done, demonstrating even more aeronautical principles, like airfoil design; tail plane ascent and descent action; control column; the respective action of the rudder pedals; tail and rudder action; function of flaps, spoilers and ailerons, and dihedral wing angles. To free the students from their cognitive chains, we designed, then flew, paper airplanes. These called on many of the same flight principles we had been learning. (Yes, we, I learnt as much as my young charges in researching and preparing this lesson, being as foreign to the esoteric world of flying – if not the maths involved – as they were!)
We launched our creations from various elevated places, like the school roof and the local lookout. I know; the lost planes constitute litter; but I weighted this environmental sin against the intellectual benefits my students were garnering. Anyway, in compensation we picked up papers around the site! An aspect of this educational credit was in seeing, in our test-flight successes and otherwise, the various aerodynamic laws in action, like wing size, weight, shape and proportion.
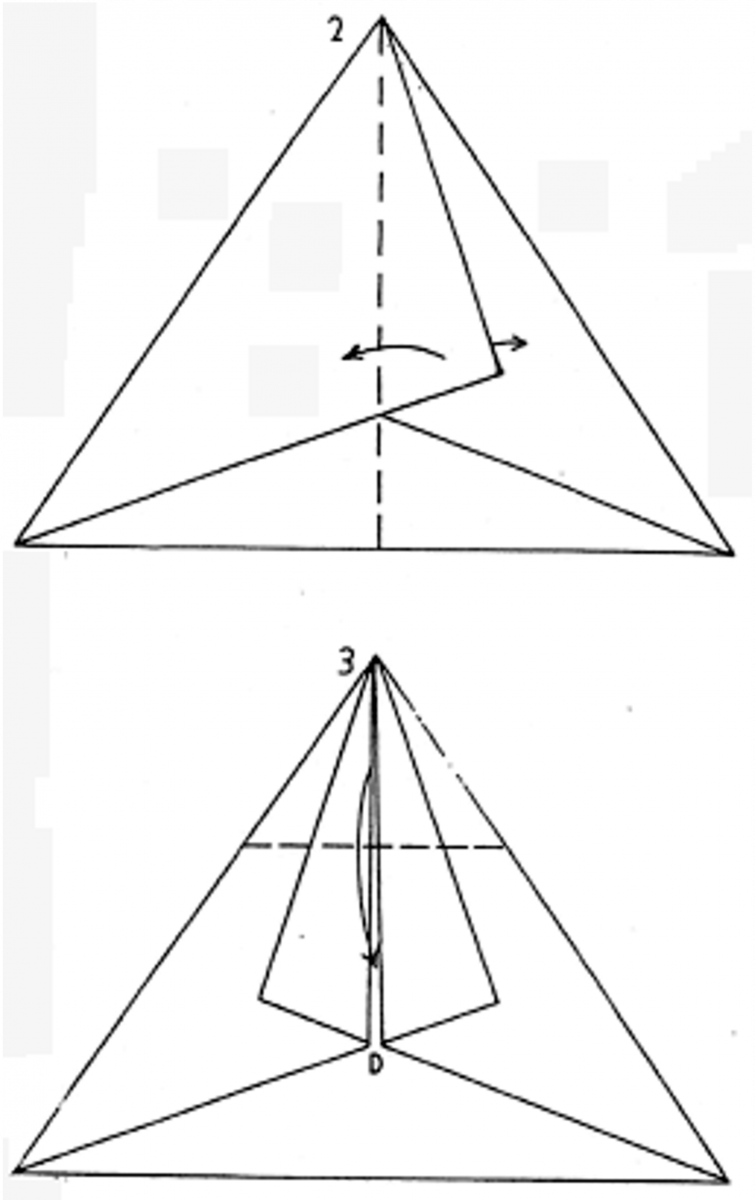
Begin with a A4 sheet of paper and fold it in half widthwise. Fold the corners in along AB and AC
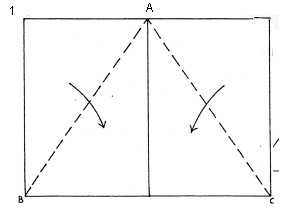
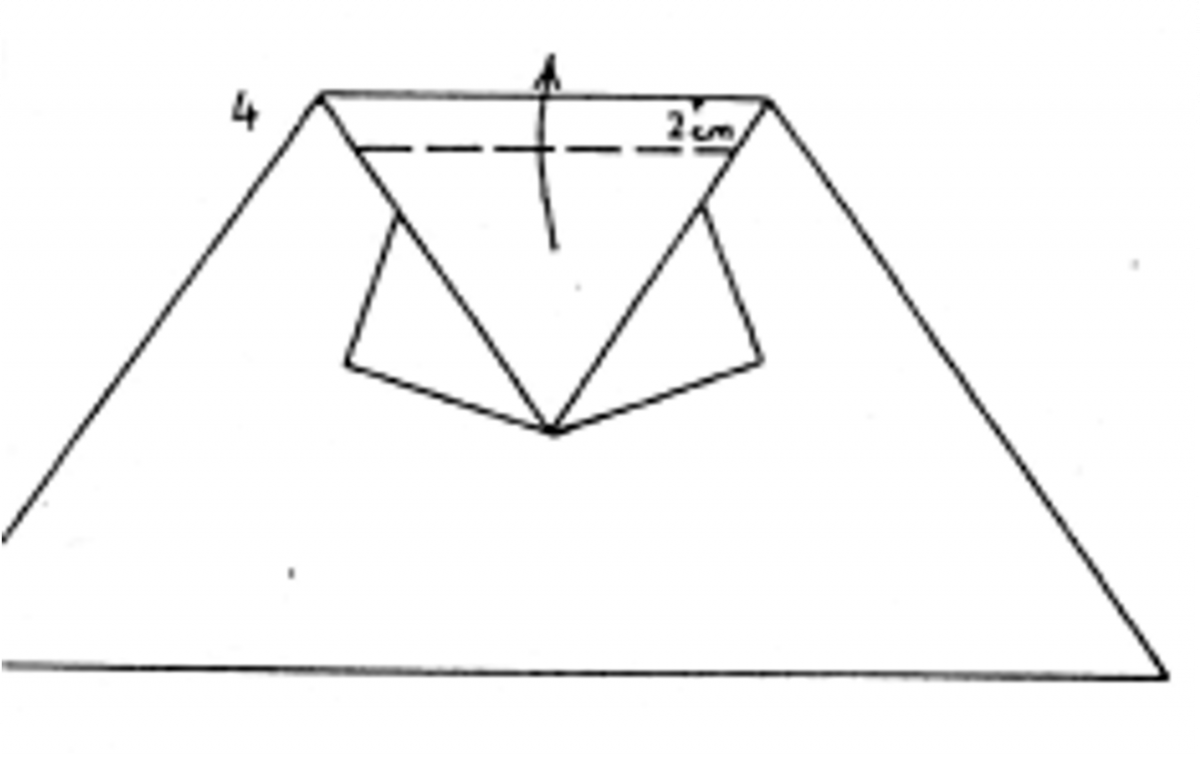
Fold the top nose down to point D. Then Fold the nose back up by tow centimeters to the top edge.
Fold the model in half.
- Grab point O with your thumb and finger and tug the nose upwards.
- Place your thumb and forefinger inside the nose., pushing into point E, to turn the fold inside out.
- Fold the nose point inside, then outside again to make a smaller point.
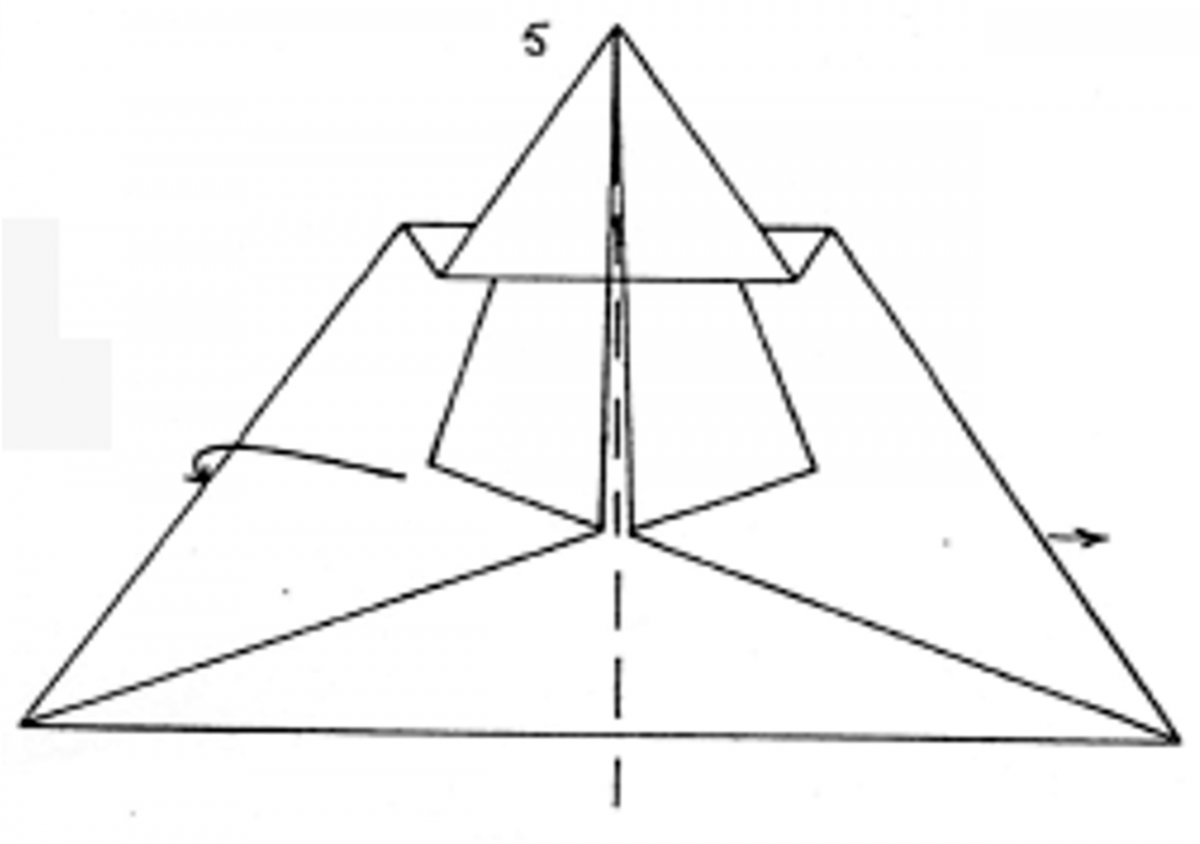
- Cut along the dotted line to make the wing shape.
- Fold the wings down on both sides along the line of dashes.
As well as flying paper airplanes, one teacher organized a model airplane making and flying 3-week block lesson to complement the Maths in Aviation. They also had a stimulating afternoon flying sophisticated remote-control model aircraft.
Information was given on wind behavior, especially in relation to hang gliding. This included (with yet more drawings, this time including an artistic element) the difference between inland and seaboard thermals, lee waves, and ridge lift. The number principles of the corkscrew propeller were also explored. The propeller is almost always 3-pronged. This, and the common triangle shape of a wing, is evidence of the omnipresent etheric element in flight, expressing the air element as it does. In fact both these 3-fold forms are used as symbols of the ether body.
The best teachers of the unit were however the masters of aviation themselves, the birds. Just like Leonardo da Vinci, we observed the avian flight of both feathered and featherless flyers at both hang gliding sites, Stanwell park and the lofty Kurnell sand dunes.
One daredevil of the non-feathered (human!) kind – a German as it turned out – would almost part the hair of my highly impressed students as he “buzzed” our small group crouching on the windswept grassy knoll. We called him The Red Baron! We knew he was German because of his heavily accented battle cries as he swept down, over and up.
We also created a series of drawings demonstrating Aspect Ratio: AR = wingspan to chord (width or wing). A ‘normal’ wing is about 11 to 5, about twice as long as it is wide. This is also the AR of a traditional kite (another good practical and fun flight exercise!). Five different airplanes were compared with five birds of similar AR. The flight functions both plane and bird were designed to perform were seen to be aerodynamically similar. These drawings were in plan/silhouette. First there was the extreme AR of a Puffin Glider (a most inaptly – named aircraft!) and the gliding efficiency of the Albatross – a very high AR of about 16:2; then a small single-engine trainer and the aerial gymnastic Willy Wagtail – 2:1.5; a long-distance Boeing 747 and the tireless Spinetailed Swift – 3:1.5. This is a bird which only has recourse to terra firma to sleep and next. Then there was the self-evident Phantom Jet and the swept-backed pinions of the Peregrine Falcon; and finally the hovering X15 fighter and the Hummingbird, almost 1:1! Hang gliders have a similar AR to the soaring birds of prey.











Leave a Reply